Machine Learning Framework for Prediction of Material Failure:
Failure prediction is utterly important in the design of mechanical components, and yet, it is a rather difficult task. Early failure detection and prevention can potentially save millions of dollars in the life-cycle of products. With that objective, we construct a Machine Learning framework for data-driven failure prediction in damage models, applied to standard-to-anomalous materials. Using pattern recognition, classification algorithms and uncertainty quantification, we can detect the presence and location of failure with robustness, even with noise-polluted data.
Photo: A pattern recognition scheme represents time-series: data of damage degradation function, with k-Nearest Neighbor and Artificial Neural Network algorithms employed for failure classification using recognized patterns. case(I), case(II) and case(III): "Representative failure cases obtained from a damage and fatigue phase-field simulation". "Confusion matrix with ANN classification results for detection of presence (no failure, onset of failure and failure), and location/pattern of failure for the three representative cases, a total of 9 classes."

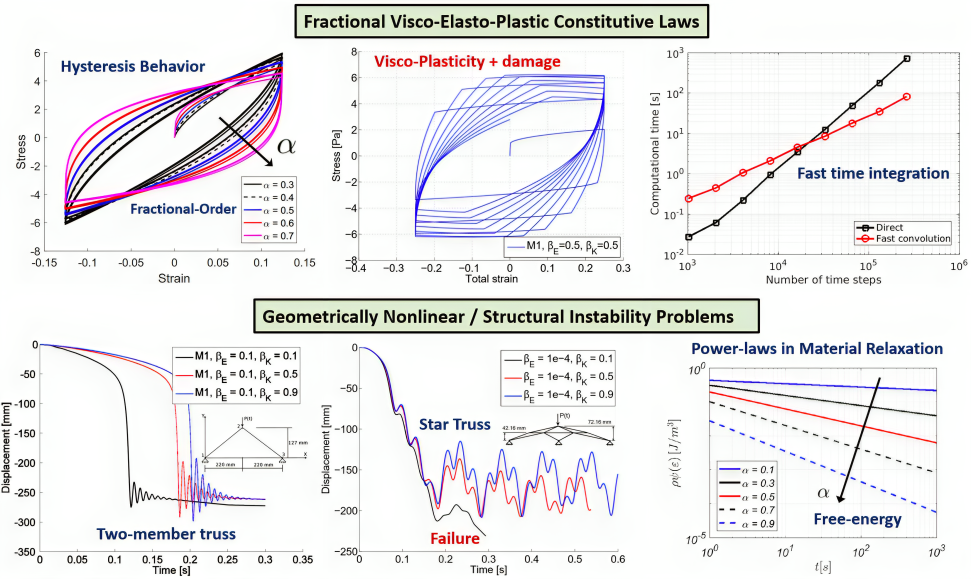
Data/Design Driven Modeling of Transport/Materials:
Construction of mathematically sound model forms for the life-cycle of a broad range of existing, and yet-to-be-developed complex materials (soft materials, bio-tissues, bio-mimetic materials). When subject to thermo-mechanical loads, these materials undergo non-Fickian diffusion processes in their ordered/disordered micro-structure, which leads to a stochastic power-law scaling observed in visco-elastic stress relaxation, plasticity, damage/aging and failure. In order to capture such effects, we make use of fractional visco-elasto-plastic models, and leverage their potential using generalized distributed-order models, describing the evolving aforementioned effects in the context of small to large strains.
Photo: (Top) Fractional modeling of visco-elastic materials. (Bottom) Truss-like structures with complex material behavior.
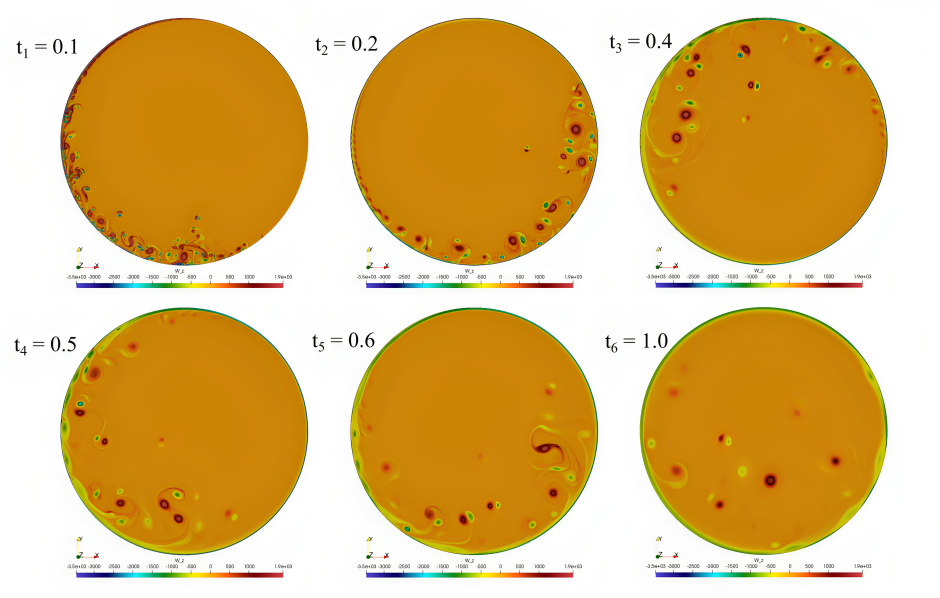
Fractional Scalar Turbulence:
Scalar mixing by a turbulent flow is of interest to model pollutants dispersion, reactive flows, and industrial processes. Due to the anomalous features of turbulence, we propose a new stochastic framework of turbulence modeling by employing fractional PDEs as an Eulerian approach to incorporate the nonlocal effects. There is a great consistency between the Lagrangian and Eulerian fractional modeling of scalar dispersion in the context of an isotropic turbulent flow. We are also extending the idea to model the memory effects in turbulent mixing.
Photo: Contours of (top left) scalar concentration and (bottom left) density of particle numbers in the isotropic homogeneous turbulent flow with Re = 200 and Sc = 1, employing a fractional model at t = 1 sec, Contours of (top right) scalar concentration and (bottom right) density of particle numbers in the isotropic homogeneous turbulent flow with Re = 200 and Sc = 1, employing a fractional model at t = 2 sec

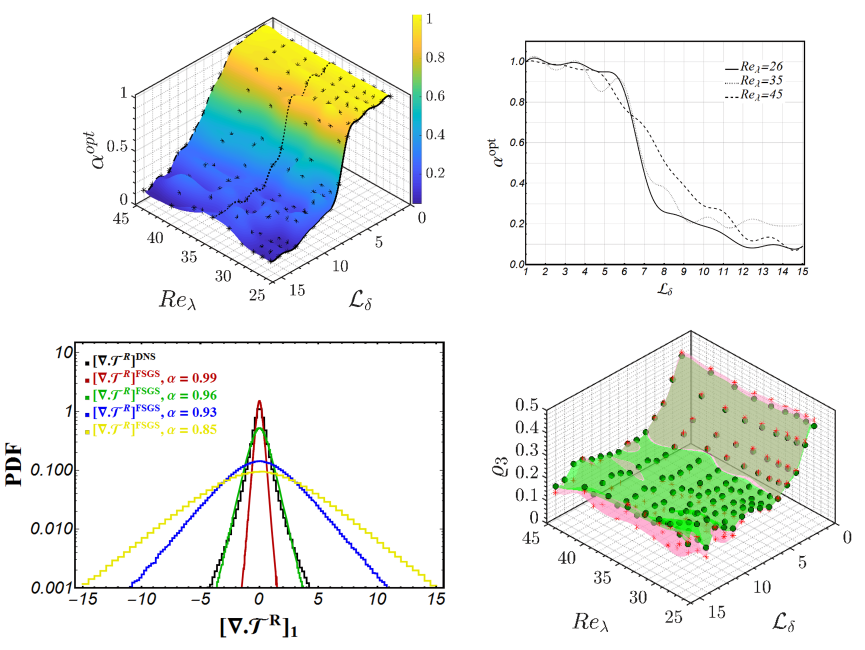
Fractional Subgrid-Scale (FSGS) Modeling:
Supported by several numerical and empirical studies, SGS motions are characterized by the intermittent structures and anomalous scaling properties in turbulent flows. Such anomalous features become even more pronounced when the filter-width enlarges. That inspires the development of new nonlocal closure models, which captures anomalous scalings of turbulent structure functions. We outline a new data-infused framework for fractional modeling of SGS motions in turbulent flows, starting from the kinetic transport equation. Within the proposed framework, we begin with modeling the filtered equilibrium distribution function as the source of SGS motions at the kinetic level. We derive the filtered NS equations from the filtered Boltzmann transport equation, in which the divergence of SGS stresses is modeled via a fractional operator. On the strong background of DNS dataset, we perform model calibration by using machine learning techniques for the associated fractional exponents. The calibration of model parameters set the ground for optimizing the efficiency of the fractional models in terms of the filter width and flow Reynolds number.
Photo: Fractional subgrid-scale (FSGS) modeling for turbulent flows.
Stochastic Modeling and Uncertainty Quantification:
In the life-cycle of complex materials, randomness is present and is propagated throughout the space and time scales. In additive manufacturing, the input parameters highly influence the thermo-fluid processes, such as the cooling rates, which lead to uncertainties in the final form of the microstructure, and consequently the material properties. In this sense, we mitigate and propagate these model uncertainties in manufacturing from micro- to macro-scale, allowing us to determine the uncertainty and reliability of the fractional operators. This aids in the selection of the appropriate constitutive model forms for describing visco-elasto-plastic behavior with damage/fatigue, and also allows better description of the uncertainty bounds of material properties and probability of failure in such materials.Scalar mixing by a turbulent flow is of interest to model pollutants dispersion, reactive flows, and industrial processes. Due to the anomalous features of turbulence, we propose a new stochastic framework of turbulence modeling by employing fractional PDEs as an Eulerian approach to incorporate the nonlocal effects. There is a great consistency between the Lagrangian and Eulerian fractional modeling of scalar dispersion in the context of an isotropic turbulent flow. We are also extending the idea to model the memory effects in turbulent mixing.
Photo: Expected value for the evolution of vorticity field in a rotating incompressible flow system with imperfect brake stochastic model. (The forward problem employs high-fidelity spectral element method to simulate each realization.)
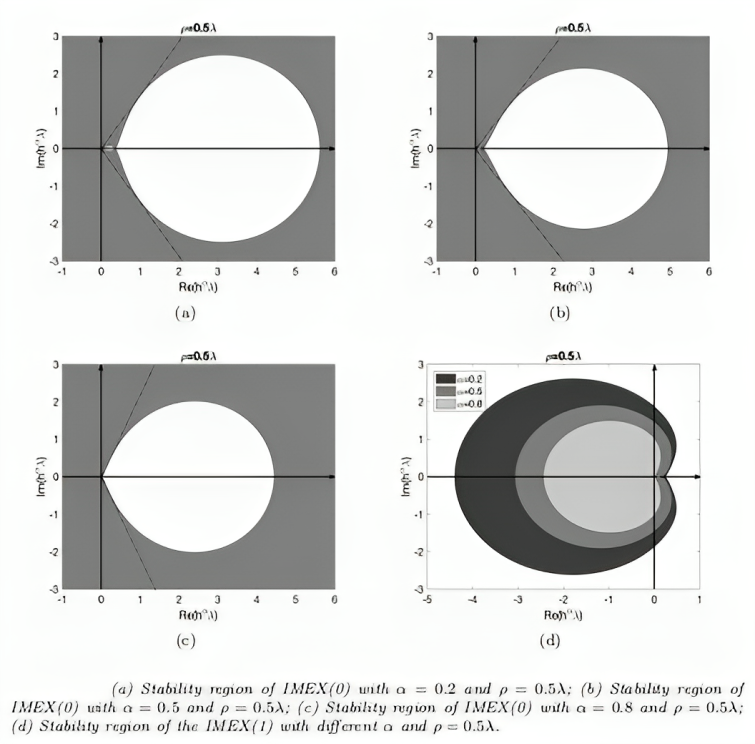
Numerical Analysis of Fractional PDEs:
Development of spectral collocation methods for time- and space- fractional differential equations (constant, variable and distributed orders), and fast time-fractional multi-step integration schemes with lower computational complexity to allow the application of FPDEs to large-scale systems. We also develop spectrally-accurate schemes for fixed-to-distributed order fractional partial differential equations in time and space and also fast time-fractional multi-step integration schemes with lower computational complexity to allow the application of FPDEs to large-scale systems.